Äquivalenz Von Masse Und Energie

Aus dem Jahre 1946 stammt ein (handgeschriebener) Aufsatz von Albert Einstein in dem in allgemein verständlicher Form dice Aussage der Formel Eastward = m·cⁱⁱ erläutert wird.

In der vor-relativistischen Physik gab es zwei voneinander unabhängige Erhaltungs- bzw. Bilanzgesetze, dice strenge Gültigkeit beanspruchten, nämlich

i) den Satz von der Erhaltung der Energie,

2) den Satz von der Erhaltung der Masse.

Der Satz von der Erhaltung der Energie, welcher schon im 17. Jahrhundert von Leibnitz in seiner vollen Allgemeinheit als gültig verwendet wurde, entwickelte sich im 19. Jahrhundert wesentlich als eine Folge eines Satzes der Mechanik.

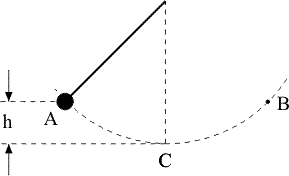
Man betrachte ein Pendel, dessen Masse zwischen den Punkten A und B hin und her schwingt. In A (und B) verschwindet dice Geschwindigkeit v, und dice Masse thousand steht um h höher als im tiefsten Punkte C der Bahn. In C ist diese Hubhöhe verloren gegangen, dafür aber hat die Masse hier eine Geschwindigkeit five. Es ist, wie wenn sich Hubhöhe in Geschwindigkeit und umgekehrt restlos verwandeln könnten. Die exakte Beziehung ist

\[thousand \cdot g \cdot h = k \cdot \frac{{{v^two}}}{2}\]

wobei g die Beschleunigung der Erdschwere bedeutet. Das Interessante dabei ist, dass diese Beziehung unabhängig ist von der Länge des Pendels und überhaupt von der Form der Bahn in welcher die Masse geführt wird. Interpretation: Es gibt ein Etwas (nämlich die Energie), das während des Vorgangs erhalten bleibt.

In A ist dice Energie eine Energie der Lage oder „potentielle Energie", in C eine Energie der Bewegung oder „kinetische Energie". Wenn diese Auffassung das Wesen der Sache richtig erfasst, and so muss die Summe

\[m \cdot g \cdot h + g \cdot \frac{{{five^2}}}{2}\]

auch für alle Zwischenlagen denselben Wert haben, wenn man mit h die Höhe über C und mit v die Geschwindigkeit in einem beliebigen Punkte der Bahn bezeichnet. Dies verhält sich in der Tat and then. Die Verallgemeinerung dieses Satzes gibt den Satz von der Erhaltung der mechanischen Energie. Wie aber, wenn das Pendel schliesslich durch Reibung zur Ruhe gekommen ist? Davon später.

aus Einstein Archives online

Beim Studium der Wärme-Leitung war human being zu richtigen Ergebnissen gekommen unter Zugrundelegung der Annahme, dass die Wärme ein unzerstörbarer Stoff sei, der vom wärmeren zum kälteren Stoff fliesst. Es schien einen "Satz von der Erhaltung der Wärme" zu geben. Andererseits aber waren seit undenklichen Zeiten Erfahrungen bekannt, nach denen durch Reibung Wärme erzeugt wird (Feuerzeug der Indianer). Nachdem sich die Physiker lange dagegen gesträubt hatten, eine solche Erzeugung von "Wärme" zuzugeben, gelang es schliesslich zu zeigen, dass zur Erzeugung einer Wärmemenge durch Reibung immer ein genau proportionaler Betrag von mechanischer Energie aufgewendet werden muss. So z.B. beim Pendel, dessen mechanische Energie durch Reibung allmählich in Wärme übergeht. Dadurch wurden die Sätze von der Erhaltung der mechanischen und der thermischen Energie zu einem einzigen Satz verschmolzen. Hier angelangt drängte sich den Physikern die Überzeugung auf, dass dies Erhaltungsgesetz auch auf dice chemischen und elektromagnetischen Vorgänge auszudehnen sei, welche Vermutung sich bisher auf allen Gebieten mit Erfolg durchführen liess: In einem von der Aussenwelt abgeschlossenen physikalischen Organisation gibt es eine Summe von Energien, welche bei allen auftretenden Veränderungen konstant bleibt.

Nun zum Satz von der Erhaltung der Masse. Die Masse ist definiert durch den Widerstand, den ein Körper seiner Beschleunigung entgegensetzt (träge Masse). Sie wird auch gemessen durch das Gewicht des Körpers (schwere Masse). Dass diese zwei and so verschiedenen Definitionen zu derselben Masszahl für die Masse eines Körpers führen, ist eine an sich höchst verwunderliche Tatsache, deren tiefere Bedeutung erst durch die allgemeine Relativitätstheorie aufgeklärt wurde. Der Satz (zur Erhaltung der Masse) lautet: Die Massen bleiben bei irgend welchen physikalischen (und chemischen) Veränderungen ungeändert. Die Masse schien so die eigentlich wesentliche (weil invariante) Qualität der Materie zu sein. Bei Erwärmung, Schmelzen, Verdampfen, Auflösen, beim Eingehen chemischer Verbindungen ändert sich die Masse (bzw. die Gesamtmasse) nicht.

Dieser Erhaltungssatz der Masse, dem dice Physik bis vor einigen Jahrzehnten exakte Gültigkeit zugeschrieben hat, wurde durch dice spezielle Relativitätstheorie als unzureichend erkannt. Er wurde durch diese Theorie mit dem Energieprinzip in einer ähnlichen Weise zu einer Einheit verschmolzen wie etwa threescore Jahre früher der Erhaltungssatz der mechanischen Energie und der der Erhaltung der Wärmemenge miteinander verschmolzen wurden. Besser könnte man sagen: der Satz von der Erhaltung der Energie hat ehedem den der Erhaltung der Wärme und neuerdings den der Erhaltung der Masse geschluckt und hat so allein das Feld behauptet.

Den Satz von der Äquivalenz von Masse und Energie pflegt human being (etwas ungenau) durch die Formel E = thou·c^two auszudrücken, wobei c dice Lichtgeschwindigkeit (three·10^x cm/s) bedeutet. E ist die Energie, welche in einem (ruhenden) Körper steckt, m seine Masse. Die Energie, die zu der Masse m gehört, ist gleich dieser Masse, multipliziert mit dem Quadrat der ungeheuer grossen Lichtgeschwindigkeit, besides ein gewaltiger Betrag per Masseneinheit.

Nun mag man erstaunt fragen: Wie kommt es denn, dass human von dieser ungeheueren Energie, die in jedem Gramm Materie steckt, bisher so gar nicht bemerkt hat? Dice Antwort ist einfach: solange von dieser Energie nichts nach aussen weggegeben wird, kann human being ihr ihre Energie-Natur nicht anmerken. Es ist wie bei einem reichen Manne, der kein Geld ausgibt; wie soll human being ihm seinen Reichtum anmerken?

Nun kann man auch die Beziehung umdrehen und sagen, dass mit einer Energiezunahme Eastward eine Massenzunahme E/cⁱⁱ verbunden sein muss. Energie kann ich aber der Masse leicht zuführen, z. B. indem ich sie um 10 Grad erwärme. Warum also nicht die damit verbundene Massenzunahme (bzw. Gewichtszunahme) messen? Das böse an diesem Geschäft ist, dass in der Massenzunahme der ungeheure Faktor c² im Nenner auftritt. Dies bedeutet, dass dice Massenzunahme in einem solchen Falle vie zu klein ist, um direkt z.B. mit Hilfe einer empfindlichen Waage gemessen zu werden.

Damit also eine Massenzunahme sich in messbarer Quantität zeige, muss die Änderung der Energie pro Masseneinheit ungeheuer gross sein. Wir kennen nur ein einziges Erscheinungsgebiet, in welchem ungeheuere Energieänderungen pro Masseneinheit frei werden, nämlich beim radioaktiven Zerfall. Schematisch ist ein solcher Vorgang von folgender Art. Ein Atom der Masse M spaltet sich in zwei Atome von der Masse M′ bzw. M′′, welche mit gewaltiger Energie auseinander fahren. Denkt man sich diese zwei Massen zur Ruhe gebracht, d.h. entzieht human being ihnen diese kinetische Energie, so sind sie zusammen genommen wesentlich energie-ärmer, als das ursprüngliche Atom gewesen ist. Dies bewirkt nach dem Äquivalenz-Satz, dass auch die Massensumme M' + M'' der Zerfallsprodukte etwas kleiner sein muss als dice ursprüngliche Masse M des radioaktiv zerfallenden Atoms (ein Widerspruch mit dem alten Erhaltungssatz der Masse). Der relative Unterschied beider erreicht dice Grössenordnung eine zehntel Prozent.

Nun kann man zwar die Atom nicht einzeln wiegen. Aber es gibt empfindliche indirekte Methoden zur genauen Messung des Atomgewichtes auf dice wir hier nicht näher einzugehen brauchen. Ebenso kann human durch indirekte Methoden die kinetischen Energien bestimmen, welche beim Zerfall auf die Zerfallsprodukte Thou' und M'' übertragen werden. And so ist es möglich gewesen, die Äquivalenz-Formel zu prüfen und zu festigen. Auch erlaubt das Gesetz aus genau bestimmten Atomgewichten vorauszuberechnen, wie viel Energie bei einem ins Auge gefassten Atomzerfall frei wird. Das Gesetz sagt aber natürlich nichts darüber aus, ob und wie eine ins Auge gefasst Zerfall-Reaktion herbeigeführt werden kann.

Was bei dem radioaktiven Zerfall mit der Masse bzw. Energie des Atoms Yard geschieht, lässt sich an dem oben erwähnten reichen Manne so illustrieren. Thou ist ein reicher Geizhals, der zu seinen Lebzeiten überhaupt kein Geld (Energie) ausgab. Im Falle seines Todes hinterlässt er alles seinen Söhnen One thousand′ und Yard′′ jedoch mit der Verpflichtung einen ganz geringen Betrag, nämlich weniger als ein Promille der Riesenerbschaft (Energie bzw. Masse) an die Gemeinde abzugeben. Dice Söhne haben dann zusammen genommen etwas weniger als der Vater besessen hatte (dice Massensumme M′ + Thou′′ ist etwas kleiner als die Masse M des radioaktiven Atoms). Der prozentisch so geringe Anteil, der an die Gemeinde abgeliefert wird, ist jedoch (in seiner Äusserungsform als kinetische Energie betrachtet) and so ungeheuer gross, dass er das ganze Unheil mit sich bringt, das abzuwenden das dringendste Problem unserer Zeit geworden ist.

Source: https://www.leifiphysik.de/relativitaetstheorie/spezielle-relativitaetstheorie/ausblick/aequivalenz-energie-masse

Posted by: koehlertallean.blogspot.com